The NLMIXED Procedure
Compartment Models
Pharmacokinetics (PK) is a branch of medicine that models the movement of a drug through the body (Gabrielsson and Weiner 2006). PK is sometimes referred to as the study of what the body does to a drug. Compartment models are basic building blocks of PK models. In a study, a body is divided in to several compartments, groups of organs or tissues that are kinetically homogeneous. The main interest of PK is to model how a drug moves through these compartments—for example, to estimate the amount of a drug and further concentrations of the drug that are present in a compartment at any given time. The concentrations of the drug, over time, are typically modeled via a set of differential equations that depend on a variety of variables, such as the amount of drug given, elimination rates, transfer rates, and so on. The sets of differential equations can also depend on how the drug is administered to the body, distributed through the body, and eliminated from the body. These models are known as compartment models, which are divided based on the number of compartments. Not all analytical solutions to multiple-compartment differential equations models are known, but Abuhelwa, Foster, and Upton (2015) and Fisher and Shafer (2007) provide closed-form solutions for those that correspond to the one-, two-, and three- compartments. These are the models that are handled by the CMPTMODEL statement.
Routes of Drug Administration
There are three types of drug administration methods: intravenous bolus, intravenous infusion, and extravascular dose administrations. A bolus medication typically has no or a very short time lag for the drug to enter a compartment. Intravenous infusions are given over a period of time, and the drug enters into the body at a constant rate. In infusion, the two quantities, rate and duration of the infusion, are of interest and are used in calculating the amount of drug present in the body. The rate and the duration of the infusion are related, so knowing one determines the other. For compartment models that have infusion type of administration, it is sufficient to provide either the rate or the duration information.
One-, Two-, and Three-Compartment Models for Intravenous Administration
This section lists a number of assumptions that are made on the set of compartment models that the CMPTMODEL statement supports. The one-, two-, and three-compartment models all have a central compartment and can have one or more peripheral compartments that are linked only to the central compartment but not to each other. After a drug is administered to an administration site, it is distributed to the central compartment and then to other peripheral compartments. The rates at which the drug moves from the central compartment to and from the other peripheral compartments are characterized by transfer rate constants. The rates at which the drug is eliminated from the central or the peripheral compartments are characterized by elimination rate constants.
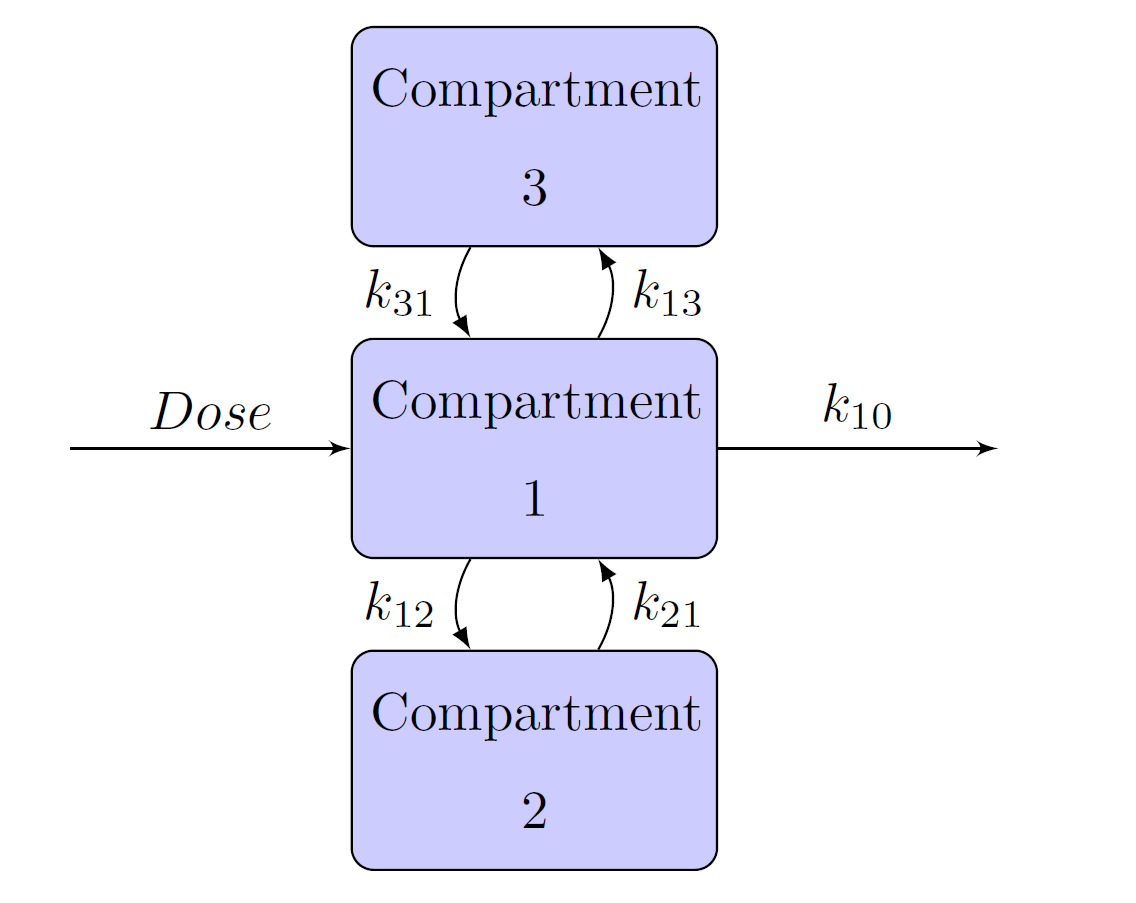
Schematic representation of the one-, two-, and three- compartment models are given in Figure 12, Figure 13, and Figure 14, respectively. In each figure, Dose is the dosage of the drug that is given intravenously, and represents the rate at which the drug is eliminated from compartment 1. In Figure 13 and Figure 14,
represents the transfer rate constant from compartment 1 to compartment 2 and
represents the transfer rate constant from compartment 2 to compartment 1. Similarly, in Figure 14,
represents the transfer rate constant from compartment 1 to compartment 3 and
represents the transfer rate constant from compartment 3 to compartment 1. In these scenarios, compartment 1 is the central compartment and compartments 2 and 3 are the peripheral compartments. In compartment models, a drug can be administered only to and eliminated only from the central compartment.
Figure 12: One-Compartment Model
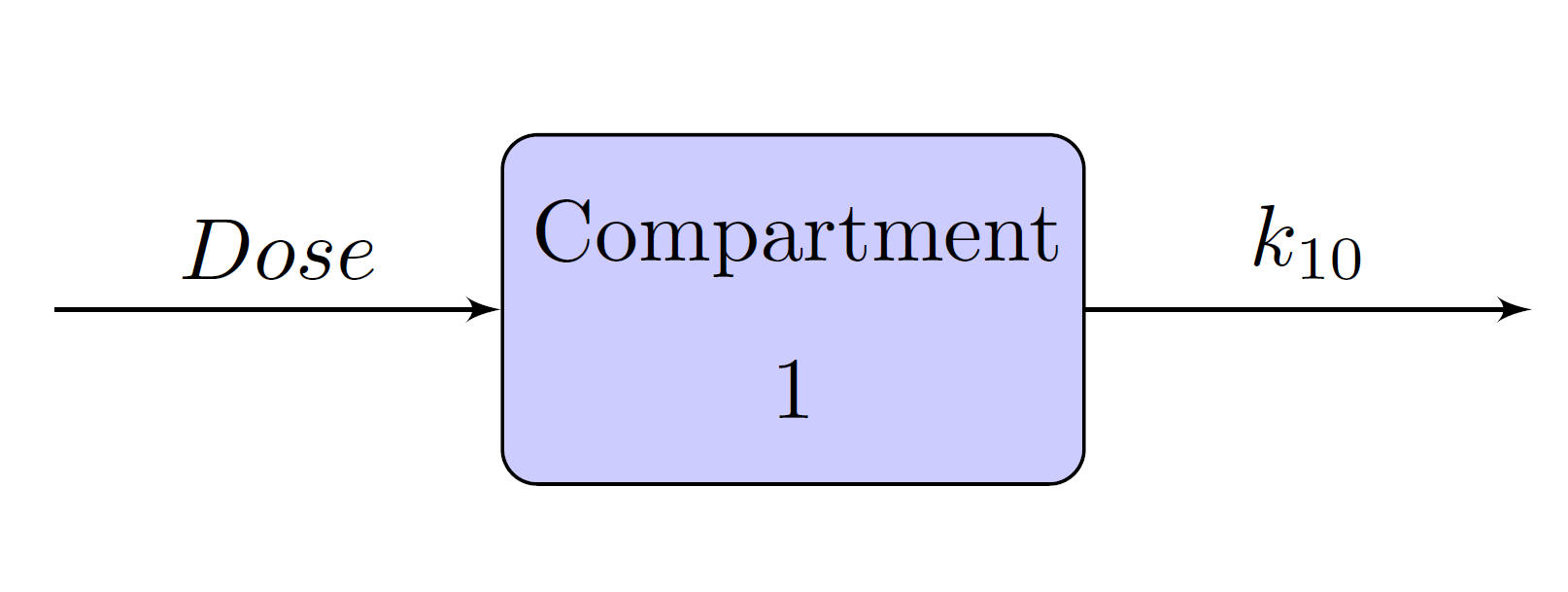
Figure 13: Two-Compartment Model

Figure 14: Three-Compartment Model
One-, Two-, and Three-Compartment Models for Extravascular Administration
Extravascular administrations, such as oral administration, are different from bolus and infusion in the sense that there is an absorption phase before the drug enters the central compartment. Schematic representation of the one-, two-, and three- compartment models when the drug is administered using an oral method are given in Figure 15, Figure 16, and Figure 17, respectively. In these models, compartment 0 is also called the depot compartment.
Figure 15: One-Compartment Model with Absorption Phase
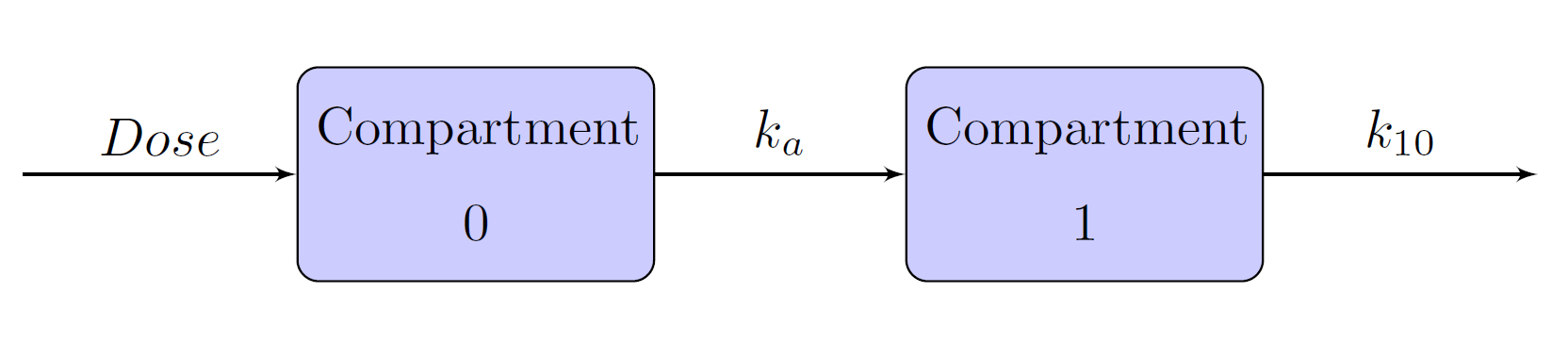
Figure 16: Two-Compartment Model with Absorption Phase
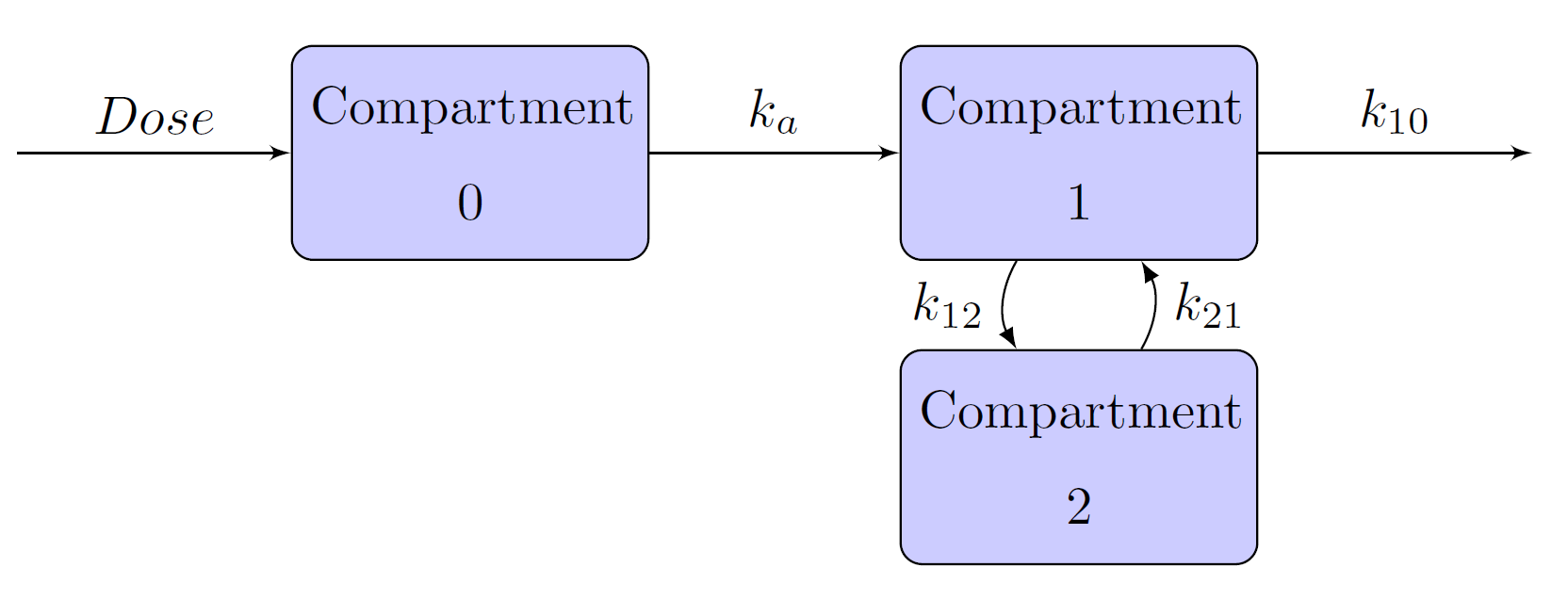
Figure 17: Three-Compartment Model with Absorption Phase

Compartment Models Specification
The CMPTMODEL statement in PROC NLMIXED enables you to fit one-, two-, and three-compartment models that use bolus, infusion, or oral types of drug administration. The CMPTMODEL statement computes the predicted concentrations of the drug for all compartments at each time point.
The CMPTMODEL statement supports a large number of options, which are grouped into three types: required, conditionally-required, and optional options. You use the required options to specify the type of compartment model that you want to fit (the NCOMPS=, ADMTYPE=, and PARMTYPE= options) and to provide the input time variable (in the TIME= option) and the outcome variable (in the PCONC= option) that is the predicted concentration in the first (central) compartment at each time point.
The statement supports the following nine types of compartment models:
one-compartment model with bolus dose administration
one-compartment model with infusion type of dose administration
one-compartment model with oral dose administration
two-compartment model with bolus dose administration
two-compartment model with infusion type of dose administration
two-compartment model with oral dose administration
three-compartment model with bolus dose administration
three-compartment model with infusion type of dose administration
three-compartment model with oral dose administration.
Each of these nine models can be parameterized in two ways: in terms of elimination and transfer rate constants of each compartment, or in terms of clearance and volume parameters of each compartment. The relationship between rate constants and the clearance and volumes of each compartment are:
where CLn and VOLn are the clearance and volume of the nth compartment for n=1,2,3. You can use the PARMTYPE= option in the CMPTMODEL statement to specify these parameterizations. In total, you can specify 18 types of compartment models by using combinations of the NCOMPS=, ADMTYPE=, and PARMTYPE= options in the CMPTMODEL statement.
The conditionally required options define the specifics needed in some of the compartment models. For example, if you specify a two-compartment model with a bolus type of drug administration in terms of rate constants by using NCOMPS=2, ADMTYPE=IVB, and PARMTYPE=1, then you must specify the K12=, K21=, and K10= options. Here is an example:
PROC NLMIXED data=TwoComp;
...other statements...
erate10= exp(beta1);
trate12= exp(beta2);
trate21= exp(beta3);
CMPTMODEL ncomps=2 admtype=ivb parmtype=1 pconc=pred time=time
k10=erate10 k12=trate12 k21=trate21
dose1=ddose scale1=vol/1000;
model conc ~ normal(pred,s2);
...other statements...
run;
The K12= and K21= options specify the transfer rate constants, and the K10= option specifies the elimination rate constant from the central compartment. In addition, you can specify dosage information (DOSEn=) or scaling information (SCALEn=) in the syntax. For more information, see the section CMPTMODEL Statement.
Table 2, Table 3, and Table 4 list all conditionally required options and valid optional options for each of the 18 compartment models.
Table 2: One-Compartment Models
| Model | Required | Conditionally Required |
Optional |
|---|---|---|---|
| One compartment with bolus dose |
NCOMPS=1 ADMTYPE=IVB PARMTYPE=1 |
K10= | DOSE1= SCALE1= |
| One compartment with bolus dose |
NCOMPS=1 ADMTYPE=IVB PARMTYPE=2 |
CL1= VOL1= | DOSE1= SCALE1= |
| One compartment with infusion dose |
NCOMPS=1 ADMTYPE=INF PARMTYPE=1 |
K10= RATE= (or) DURN= |
DOSE1= SCALE1= |
| One compartment with infusion dose |
NCOMPS=1 ADMTYPE=INF PARMTYPE=2 |
CL1= VOL1= RATE= (or) DURN= |
DOSE1= SCALE1= |
| One compartment with oral dose |
NCOMPS=1 ADMTYPE=ORAL PARMTYPE=1 |
K10= Ka= | DOSE1= SCALE1= |
| One compartment with oral dose |
NCOMPS=1 ADMTYPE=ORAL PARMTYPE=2 |
CL1= VOL1= Ka= | DOSE1= SCALE1= |
Table 3: Two-Compartment Models
| Model | Required | Conditionally Required |
Optional |
|---|---|---|---|
| Two compartments with bolus dose |
NCOMPS=2 ADMTYPE=IVB PARMTYPE=1 |
K10= K12= K21= | DOSE1= DOSE2= SCALE1= SCALE2= K20= PCONC2= |
| Two compartments with bolus dose |
NCOMPS=2 ADMTYPE=IVB PARMTYPE=2 |
CL1= VOL1= CL2= VOL2= |
DOSE1= DOSE2= SCALE1= SCALE2= K20= PCONC2= |
| Two compartments with infusion dose |
NCOMPS=2 ADMTYPE=INF PARMTYPE=1 |
K10= K12= K21= RATE= (or) DURN= |
DOSE1= SCALE1= |
| Two compartments with infusion dose |
NCOMPS=2 ADMTYPE=INF PARMTYPE=2 |
CL1= VOL1= CL2= VOL2= RATE= (or) DURN= |
DOSE1= SCALE1= |
| Two compartments with oral dose |
NCOMPS=2 ADMTYPE=ORAL PARMTYPE=1 |
K10= K12= K21= Ka= |
DOSE1= DOSE2= SCALE1= SCALE2= K20= PCONC2= |
| Two compartments with oral dose |
NCOMPS=2 ADMTYPE=ORAL PARMTYPE=2 |
CL1= VOL1= CL2= VOL2= Ka= |
DOSE1= DOSE2= SCALE1= SCALE2= K20= PCONC2= |
Table 4: Three-Compartment Models
| Model | Required | Conditionally Required |
Optional |
|---|---|---|---|
| Three compartments with bolus dose |
NCOMPS=3 ADMTYPE=IVB PARMTYPE=1 |
K10= K12= K21= K13= K31= |
DOSE1= DOSE2= DOSE3= SCALE1= SCALE2= SCALE3= K20= K30= PCONC2= PCONC3= |
| Three compartments with bolus dose |
NCOMPS=3 ADMTYPE=IVB PARMTYPE=2 |
CL1= VOL1= CL2= VOL2= CL3= VOL3= |
DOSE1= DOSE2= DOSE3= SCALE1= SCALE2= SCALE3= K20= K30= PCONC2= PCONC3= |
| Three compartments with infusion dose |
NCOMPS=3 ADMTYPE=INF PARMTYPE=1 |
K10= K12= K21= K13= K31= RATE= (or) DURN= |
DOSE1= SCALE1= |
| Three compartments with infusion dose |
NCOMPS=3 ADMTYPE=INF PARMTYPE=2 |
CL1= VOL1= CL2= VOL2= CL3= VOL3= RATE= (or) DURN= |
DOSE1= SCALE1= |
| Three compartments with oral dose |
NCOMPS=3 ADMTYPE=ORAL PARMTYPE=1 |
K10= K12= K21= K13= K31= Ka= |
DOSE1= DOSE2= DOSE3= SCALE1= SCALE2= SCALE3= K20= K30= PCONC2= PCONC3= |
| Three compartments with oral dose |
NCOMPS=3 ADMTYPE=ORAL PARMTYPE=2 |
CL1= VOL1= CL2= VOL2= CL3= VOL3= Ka= |
DOSE1= DOSE2= DOSE3= SCALE1= SCALE2= SCALE3= K20= K30= PCONC2= PCONC3= |
One-Compartment Model with an Oral Dose Administration
Consider the example One-Compartment Model with Pharmacokinetic Data, which studies the dispersion of the theophylline drug through a living individual. In this example, Pinheiro and Bates (1995) considered an one-compartment model with an oral dose. The paper mentions the solution to the one-compartment model. Instead of using the explicit solution, you can use the CMPTMODEL statement to fit the same model as follows:
proc nlmixed data=theoph;
parms beta1=-3.22 beta2=0.47 beta3=-2.45
s2b1 =0.03 cb12 =0 s2b2 =0.4 s2=0.5;
cl = exp(beta1 + b1);
ka = exp(beta2 + b2);
ke = exp(beta3);
vl = cl/ke;
CMPTMODEL ncomps=1 admtype=oral time=time pconc=predConc
parmtype=1 ka=ka k10=ke dose0=dose scale1=vl;
model conc ~ normal(predConc,s2);
random b1 b2 ~ normal([0,0],[s2b1,cb12,s2b2]) subject=subject;
run;
The NCOMPS=1 and ADMTYPE=ORAL options specify a one-compartment model with oral administration. Time is a data set variable that indicates time, and predConc is an outcome variable that contains predicted concentration. The PARMTYPE=1 option requests the compartment model using absorption and elimination rate constants, with KA=ka and K10=ke indicating the absorption and elimination rate constants, respectively. The dosage value for each patient in the depot compartment is specified in DOSE0=option, where dose is a data set variable. Lastly, SCALE1=vl scales the predicted concentrations by vl.
Multiple Doses
In PK field experiments or observational studies, a patient can often receive a drug multiple times, either continually or periodically over a period of time. The patient can also receive multiple types of drug in a study. For example, a patient might receive a bolus injection in the morning and an infusion drug at a constant rate in the evening. Calculation of predicted concentration in each compartment in the presence of these multiple doses or multiple types of dosing is different from single-dosing compartment models. For differential equations of a number of multiple-dosage scenarios and solutions to predicted concentration for the central compartment, see Gabrielsson and Weiner (2006).
The CMPTMODEL statement handles multiple doses in one-, two-, or three-compartment models and computes predicted concentrations in the central compartment. The syntax specification does not change from single-dose models, and the structure and content of the input data set are understood by the statement to fit various types of multiple-dosage models.
Within the biopharmaceutical industry, data in multiple-dosage studies are often structured by following a convention that has been popularized by NONMEM software (Beal et al. 2011). This convention is used to name variables and specify variable values; see Owen and Fiedler-Kelly (2014). If your data are available in a SAS data set that follows this convention, the data set must be converted to a SAS data set that is suitable to be analyzed using PROC NLMIXED. You can use the autocall macro %PKCONVRT for this purpose.
The %PKCONVRT macro takes two arguments: an input data set (specified by the first argument) and an output data set (specified by the second argument). The organization of the input data set should follow the convention. The output data set can serve as the DATA= data set for PROC NLMIXED to fit single-dose or multiple-dose models. Here is a simple example:
data pk_ex;
input ID TIME AMT DV EVID;
datalines;
1 0.00 60000 . 1
1 0.20 50000 . 1
1 0.25 0 1126.1 0
1 0.50 0 869.9 0
1 0.75 0 883.6 0
1 1.00 0 1244.0 0
1 1.50 0 995.2 0
2 0.00 70000 . 1
2 0.25 0 1126.1 0
2 0.50 0 869.9 0
2 0.75 0 883.6 0
2 1.00 0 1244.0 0
.... more lines ...
;
run;
%pkconvrt(data=pk_ex, out=out_ex);
If you want to fit a two-compartment model for the preceding multiple dosage data, use the following NLMIXED program with the out_ex data set that is produced from the %PKCONVRT macro:
proc nlmixed data=out_ex;
parms beta1=2 beta2=2 beta3=2 beta4=2 s2=0.6
s2b1=0.4 s2b2=0.4 s2b3=0.4 s2b4=0.4 cb21=0.001
cb31=0.001 cb32=0.001 cb41=0.001 cb42=0.001 cb43=0.001;
bounds s2b1>0, s2b2 >0, s2b3>0, s2b4>0, s2>0;
cl1 = exp(beta1+b1);
vl1 = exp(beta2+b2);
cl2 = exp(beta3+b3);
vl2 = exp(beta4+b4);
CMPTMODEL ncomps=2 admtype=ivb parmtype=2 pconc=pred time=time
vol1=vl1 cl1=cl1 vol2=vl2 cl2=cl2
scale1=vl1;
model conc ~ normal(pred,s2);
random b1 b2 b3 b4 ~ normal([0,0,0,0],[s2b1,
cb21,s2b2,
cb31,cb32,s2b3,
cb41,cb42,cb43,s2b4]) subject = id;
run;
The CMPTMODEL statement computes the predictions only for the central compartment for multiple dosage data. Therefore, options PCONC2=, PCONC3=, and PCONC0= are not valid in a multiple dose model. In addition, the K20=, K30=, DOSE2=, DOSE3=, SCALE2=, SCALE3=, SCALE0= options are ignored.
The %PKCONVRT autocall macro computes the elapsed time (from the time that a dose is administered to the time that a concentration is measured) in scenarios for both single and multiple continuous doses. The macro writes the computed time in the data set that is specified in the OUT= option. This data set also contains all the dosage information for all the time points at which the concentrations are measured. When you specify this data set in the PROC NLMIXED statement and you specify a CMPTMODEL statement, the elapsed times and the dosage information from the data set are used directly in computing the predicted concentrations in the central compartment. As a result, the CMPTMODEL statement ignores any specified DOSE1= and TIME= options. Similarly, for absorption models (ADMTYPE = ORAL), the DOSE0= and TIME= options in the CMPTMODEL statement are ignored and overwritten with the elapsed times and the dosage information from the OUT= data set. For examples that use the %PKCONVRT autocall macro and the CMPTMODEL statement to fit various compartment models, see Kurada and Chen (2018).
In addition, the CMPTMODEL statement supports steady-state dosing scenarios (Owen and Fiedler-Kelly 2014) in one-, two-, and three-compartment models. The %PKCONVRT macro keeps track of the elapsed time and dosing information that are required in the CMPTMODEL statement to fit steady-state dose models. The %PKCONVRT autocall macro supports input data sets that have combinations of steady-state and regular dosing, single and multiple dosing. For example, your data set can contain dosing history information on patients who receive multiple regular bolus doses and others who receive a single steady-state dose. When you use the output data set from the %PKCONVRT macro as input to PROC NLMIXED, the CMPTMODEL statement properly interprets all these distinct scenarios and computes the predicted concentrations accordingly.
The %PKCONVRT macro creates new variables (such as the _CMPT_ variable) in the OUT= data set. According to SAS conventions, it is best to avoid having variables whose name begins with an underscore _ in the DATA = data set. Also programming variables in the NLMIXED program that start with _CMPT_ are reserved for the internal computations; hence, avoid programming variables names that begin with _CMPT_ .