The GLIMMIX Procedure

Example 52.20 Comparison of Predictive Margins in Multicenter Study

(View the complete code for this example.)

It is often useful to compare the average response rates of treatment groups in clinical trials. This example shows how to compute predictive margins to account for covariates distributions in such a comparison.

Consider a multicenter study that investigates the performance of two treatments. In this study, ten treatment centers are randomly selected for inclusion. At each center, patients are randomly assigned to treatment A or treatment B. One of the study goals is to compare the response rates of the treatments.

The data set multicenter, created in the following DATA step, has five variables. The variable trt identifies the two treatments. The variable marker takes a value of 1 if the patient is biomarker-positive, and 0 if the patient is biomarker-negative. The response variable is 1 if the patient responds to the treatment, and 0 if the patient does not. 

data multicenter;
   input center trt$ age marker response @@;
   datalines;
 1 A  15  0  0     1 A  28  0  0
 1 A  60  0  1     1 A  68  1  1
 1 A  23  1  0     1 A  33  1  1
 1 A  30  1  0     1 A  73  1  1
 1 A  15  1  0     1 A  34  1  0
 1 A  15  1  0     1 A  68  1  1
 1 B  53  0  1     1 B  62  0  1
 1 B  15  0  0     1 B  28  1  0
 1 B  27  1  0     1 B  45  1  0
 1 B  56  1  1     1 B  24  1  0
 1 B  42  1  0     1 B  61  1  0
 1 B  15  1  0     1 B  67  1  1
 2 A  28  0  1     2 A  43  0  1
 2 A  52  0  1     2 A  49  1  1
 2 A  59  1  1     2 A  32  1  1
 2 A  50  1  1     2 A  41  1  1
 2 A  21  1  0     2 A  62  1  1
 2 A  77  1  1     2 A  70  1  1
 2 B  79  0  1     2 B  49  0  1
 2 B  73  0  1     2 B  73  1  1
 2 B  78  1  1     2 B  61  1  1
 2 B  78  1  1     2 B  54  1  1
 2 B  51  1  1     2 B  50  1  1
 2 B  17  1  0     2 B  15  1  0
 3 A  20  0  0     3 A  18  0  1
 3 A  32  0  1     3 A  55  1  1
 3 A  51  1  1     3 A  58  1  1
 3 A  36  1  1     3 A  15  1  0
 3 A  21  1  0     3 A  24  1  1
 3 A  40  1  1     3 A  28  1  0
 3 B  54  0  1     3 B  64  0  1
 3 B  15  0  0     3 B  15  1  0
 3 B  76  1  1     3 B  39  1  1
 3 B  48  1  0     3 B  34  1  0
 3 B  17  1  0     3 B  37  1  0
 3 B  35  1  0     3 B  30  1  1
 4 A  74  0  1     4 A  78  0  1
 4 A  15  1  0     4 A  41  1  1
 4 A  25  1  0     4 A  31  1  0
 4 A  22  1  0     4 A  15  1  0
 4 B  77  0  1     4 B  33  0  0
 4 B  21  1  0     4 B  15  1  0
 4 B  70  1  1     4 B  54  1  0
 4 B  15  1  0     4 B  15  1  0
 5 A  21  0  1     5 A  72  0  1
 5 A  28  1  1     5 A  58  1  1
 5 A  39  1  1     5 A  41  1  1
 5 A  35  1  0     5 A  59  1  1
 5 B  73  0  1     5 B  15  0  0
 5 B  46  1  1     5 B  59  1  1
 5 B  20  1  0     5 B  66  1  1
 5 B  24  1  0     5 B  15  1  0
 6 A  25  0  0     6 A  15  0  0
 6 A  63  1  1     6 A  15  1  0
 6 A  61  1  1     6 A  73  1  1
 6 A  35  1  0     6 A  76  1  1
 6 B  76  0  1     6 B  15  0  0
 6 B  15  1  0     6 B  15  1  0
 6 B  15  1  0     6 B  47  1  0
 6 B  77  1  1     6 B  17  1  0
 7 A  27  0  0     7 A  18  0  0
 7 A  18  0  1     7 A  62  1  1
 7 A  30  1  0     7 A  25  1  0
 7 A  40  1  0     7 A  18  1  0
 7 A  16  1  0     7 A  17  1  0
 7 A  43  1  1     7 A  24  1  0
 7 B  64  0  1     7 B  29  0  0
 7 B  23  0  0     7 B  20  1  0
 7 B  36  1  0     7 B  46  1  0
 7 B  19  1  0     7 B  41  1  0
 7 B  23  1  0     7 B  40  1  1
 7 B  37  1  1     7 B  22  1  0
 8 A  51  0  1     8 A  85  0  1
 8 A  16  1  1     8 A  37  1  1
 8 A  28  1  0     8 A  24  1  0
 8 A  25  1  0     8 A  17  1  0
 8 B  54  0  1     8 B  21  0  1
 8 B  23  1  0     8 B  20  1  0
 8 B  19  1  0     8 B  18  1  0
 8 B  21  1  0     8 B  22  1  0
 9 A  22  0  0     9 A  23  0  0
 9 A  33  1  0     9 A  68  1  1
 9 A  42  1  1     9 A  51  1  1
 9 A  16  1  0     9 A  52  1  1
 9 B  77  0  1     9 B  16  0  0
 9 B  42  1  0     9 B  59  1  1
 9 B  28  1  0     9 B  33  1  0
 9 B  31  1  0     9 B  20  1  0
10 A  30  0  1    10 A  24  0  1
10 A  18  1  0    10 A  16  1  0
10 A  27  1  1    10 A  29  1  1
10 A  40  1  1    10 A  64  1  1
10 B  32  0  1    10 B  25  0  0
10 B  19  1  0    10 B  22  1  0
10 B  23  1  0    10 B  38  1  0
10 B  18  1  1    10 B  23  1  0
;

For patient j at center i, the logistic regression model is

StartLayout 1st Row 1st Column log left-brace StartFraction pi Subscript i j Baseline Over 1 minus pi Subscript i j Baseline EndFraction right-brace 2nd Column equals beta 0 plus beta Subscript upper A Baseline upper I left-parenthesis normal t normal r normal t equals normal upper A right-parenthesis plus beta Subscript upper B Baseline upper I left-parenthesis normal t normal r normal t equals normal upper B right-parenthesis 2nd Row 1st Column Blank 2nd Column plus beta Subscript plus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus beta Subscript minus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis 3rd Row 1st Column Blank 2nd Column plus beta Subscript upper A plus Baseline upper I left-parenthesis normal t normal r normal t equals normal upper A comma normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus beta Subscript upper A minus Baseline upper I left-parenthesis normal t normal r normal t equals normal upper A comma normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis 4th Row 1st Column Blank 2nd Column plus beta Subscript upper B plus Baseline upper I left-parenthesis normal t normal r normal t equals normal upper B comma normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus beta Subscript upper B minus Baseline upper I left-parenthesis normal t normal r normal t equals normal upper B comma normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis 5th Row 1st Column Blank 2nd Column plus beta 1 normal upper A normal g normal e Subscript i j plus gamma Subscript i EndLayout

where pi Subscript i j is the probability that patient j at center i has responded to the treatment; gamma Subscript i is the random effect for center i; I is the indicator function; beta Subscript upper A and beta Subscript upper B are the effects of treatments A and B, respectively; beta Subscript plus and beta Subscript minus are the effects of a positive biomarker and a negative biomarker, respectively; and finally, beta Subscript upper A plus, beta Subscript upper A minus, beta Subscript upper B plus, and beta Subscript upper B minus are the interaction effects of trt and marker.

Given this model, the predictive margin for treatment A is

StartLayout 1st Row 1st Column StartFraction 1 Over upper N EndFraction sigma-summation Underscript i equals 1 Overscript 10 Endscripts sigma-summation Underscript j equals 1 Overscript n Subscript i Baseline Endscripts g Superscript negative 1 Baseline left-parenthesis 2nd Column ModifyingAbove beta With caret Subscript 0 Baseline plus ModifyingAbove beta With caret Subscript upper A Baseline plus ModifyingAbove beta With caret Subscript plus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus ModifyingAbove beta With caret Subscript minus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis 2nd Row 1st Column Blank 2nd Column plus ModifyingAbove beta With caret Subscript 1 Baseline normal upper A normal g normal e Subscript i j Baseline plus ModifyingAbove beta With caret Subscript upper A plus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus ModifyingAbove beta With caret Subscript upper A minus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis right-parenthesis EndLayout

where n Subscript i is the number of patients at treatment center i, upper N equals sigma-summation Underscript i equals 1 Overscript 10 Endscripts n Subscript i is the number of patients in the study, and g Superscript negative 1 Baseline left-parenthesis dot right-parenthesis is the inverse logistic link function. The predictive margin for treatment A is the average predicted response rate if all patients receive treatment A.

Similarly, the predictive margin for treatment B is

StartLayout 1st Row 1st Column StartFraction 1 Over upper N EndFraction sigma-summation Underscript i equals 1 Overscript 6 Endscripts sigma-summation Underscript j equals 1 Overscript n Subscript i Baseline Endscripts g Superscript negative 1 Baseline left-parenthesis 2nd Column ModifyingAbove beta With caret Subscript 0 Baseline plus ModifyingAbove beta With caret Subscript upper B Baseline plus ModifyingAbove beta With caret Subscript plus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus ModifyingAbove beta With caret Subscript minus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis 2nd Row 1st Column Blank 2nd Column plus ModifyingAbove beta With caret Subscript 1 Baseline normal upper A normal g normal e Subscript i j Baseline plus ModifyingAbove beta With caret Subscript upper B plus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 1 right-parenthesis plus ModifyingAbove beta With caret Subscript upper B minus Baseline upper I left-parenthesis normal m normal a normal r normal k normal e normal r equals 0 right-parenthesis right-parenthesis EndLayout

This is the average predicted response rate if all patients receive treatment B.

The following statements fit the multicenter data to the logistic regression model: 

proc glimmix data=multicenter;
   class center trt marker;
   model response = trt|marker age/s dist=binary link=logit;
   random  intercept/ subject=center;
   margins trt/ diff;
   margins trt*marker/ sliceby=marker slicediff;
run;

The first MARGINS statement requests predictive margins for the two treatment groups. The DIFF option compares average treatment response rates that control for the age and biomarker distributions.

Figure 141 shows the predictive margins for treatment A and treatment B.

Figure 141: Treatment Predictive Margins

The GLIMMIX Procedure

trt Margins
trt Estimate Standard Error DF t Value Pr > |t|
A 0.4481 0.05349 178 8.38 <.0001
B 0.6296 0.04276 178 14.72 <.0001


Figure 142 shows the test of the difference between the two treatment predictive margins.

Figure 142: Difference of Treatment Margins

Differences of trt Margins
trt _trt Estimate Standard Error DF t Value Pr > |t|
A B -0.1815 0.04689 178 -3.87 0.0002


The degrees of freedom in Figure 141 and Figure 142 are the same as those in the "Type III Tests of Fixed Effect" table (not shown). Based on the p-value, you would conclude that at the 0.05 level the average response rates of treatment A and treatment B are significantly different.

The second MARGINS statement requests predictive margins for the trt*marker interaction. The results are shown in Figure 143.

Figure 143: trt*marker Predictive Margins

trt*marker Margins
trt marker Estimate Standard Error DF t Value Pr > |t|
A 0 0.3256 0.08589 178 3.79 0.0002
A 1 0.4847 0.05322 178 9.11 <.0001
B 0 0.4913 0.08996 178 5.46 <.0001
B 1 0.6612 0.04152 178 15.93 <.0001


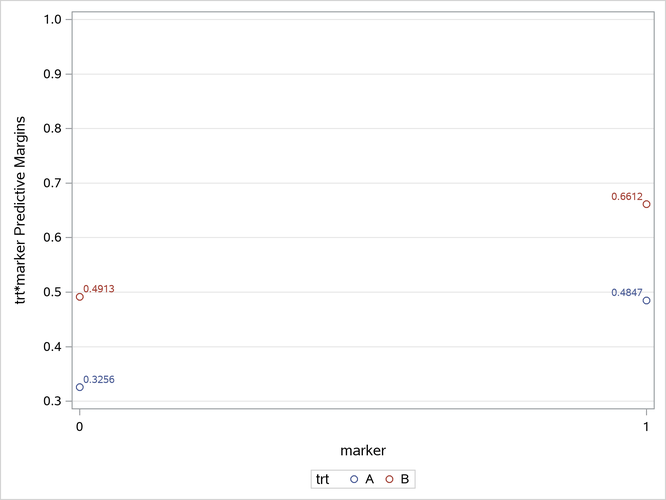
The four predictive margins in Figure 143 are plotted in Output 52.20.1.

Output 52.20.1: Predictive Margins for trt*marker

Predictive Margins for trt*marker


To test the significance of the treatment difference within each biomarker group, you can use the SLICEBY option, which slices the trt*marker interaction by the marker effect. The SLICEDIFF option then compares the sliced predictive margins for the biomarker-positive group and the biomarker-negative group separately.

Figure 144 shows the test of the treatment margin difference for the biomarker-negative group.

Figure 144: Treatment Margins Difference in Biomarker-Negative Group

Differences of trt*marker Margins Sliced by marker
Slice trt _trt Estimate Standard Error DF t Value Pr > |t|
marker 0 A B -0.1657 0.1101 178 -1.50 0.1343


Figure 145 shows the test of the treatment margin difference for the biomarker-positive group.

Figure 145: Treatment Margins Difference in Biomarker-Positive Group

Differences of trt*marker Margins Sliced by marker
Slice trt _trt Estimate Standard Error DF t Value Pr > |t|
marker 1 A B -0.1765 0.05013 178 -3.52 0.0005


Figure 145 shows that the average response rates are significantly different between treatment A and treatment B in the biomarker-positive group (p-value of 0.0005) whereas the average response rates are not significantly different in the biomark-negative group (p-value of 0.13, Figure 144).

Last updated: December 09, 2022