The CAUSALGRAPH Procedure

(View the complete code for this example.)

This example illustrates how you can use the CAUSALGRAPH procedure to quickly determine whether an adjustment set exists in a particular causal model. If an adjustment set exists, then the causal effect of the treatment variables on the outcome variables is identified. The identification implies that it is possible to estimate the specified causal effects from the data. For this reason, you might want to determine whether such a set exists, regardless of what that set might be. For more information about identifying causal effects in a causal model, see the section Causal Effect Identification.

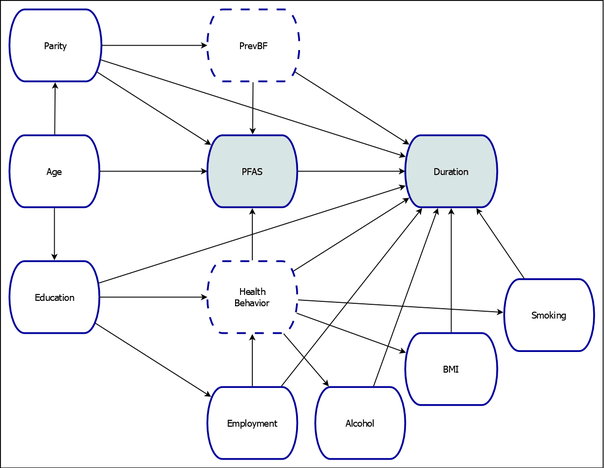
The causal model shown in Figure 6, which has been adapted from Timmermann et al. (2017), examines the relationship between maternal exposure to persistent perfluoroalkyl substances (PFAS) and breastfeeding duration among residents of the Faroe Islands. For a summary of the variables in the model, see the section Getting Started: CAUSALGRAPH Procedure. For this example, the causal model includes an additional variable, HealthBehavior, which is assumed to be a latent construct that represents the degree to which an individual’s behavior is considered to be healthful. The variables HealthBehavior and PrevBF are assumed to be unobserved, as in Timmermann et al. (2017).

Figure 6: Causal Model of the Effect of Persistent Perfluoroalkyl Substances on Breastfeeding Duration

The following statements invoke the CAUSALGRAPH procedure to determine whether it is possible to find an adjustment set that can be used to estimate the causal effect:

proc causalgraph method=adjustment maxlist=1 nosort;
   model "Timm17HealthBehavior"
      Age ==> Parity PFAS Education,
      Parity ==> PrevBF Duration PFAS,
      PrevBF ==> PFAS Duration,
      PFAS ==> Duration,
      Education ==> Duration HealthBehavior Employment,
      HealthBehavior ==> PFAS Duration BMI Alcohol Smoking,
      Employment ==> HealthBehavior Duration,
      BMI Alcohol Smoking ==> Duration;
   identify PFAS ==> Duration;
   unmeasured PrevBF HealthBehavior;
run;

In the MODEL statement, you specify the causal model to be analyzed. The quoted string in the statement labels the model. The remainder of the MODEL statement specifies all the variables and edges in the model. These variables and edges reflect the hypothesized data generating process shown in Figure 6.

In the IDENTIFY statement, you specify the causal effect of interest. You can use this statement to specify one or more treatment variables and one or more outcome variables. The treatment and outcome variables are separated by a single right arrow, ==>. In this example, you are interested in testing the identification of the causal effect of the variable PFAS on the variable Duration.

In the UNMEASURED statement, you specify variables that are not observed and thus cannot be included in an adjustment set. In this example, the variables PrevBF and HealthBehavior are unmeasured.

The METHOD=ADJUSTMENT uses the constructive backdoor criterion for identifying causal effects. The MAXLIST=1 prints only a single adjustment set. The NOSORT option specifies that it is not necessary to print the smallest adjustment sets first. These options enable the procedure to use an efficient algorithm to quickly find an adjustment set, if at least one adjustment set exists. For more information about the computational complexity of the algorithms that PROC CAUSALGRAPH uses, see the section Time Requirements.

As shown in Output 37.2.1, for the causal model in Figure 6, it is not possible to use an adjustment set to identify the effect of PFAS on Duration.

Although you cannot use an adjustment set to estimate the causal effect in Figure 6, it is still possible to estimate the causal effect if you are willing to make additional parametric assumptions in the model. See Example 37.5 for an example.